【Kivy】Pythonで落ちもの系ゲーム開発(テトリス風)Part2

こんにちは、にわこまです。
今回は、テトリミノと呼ばれる7種類のミノを作成します。また、そのミノを盤面上に固定する共通関数を作成します。7種類作成するということでコード自体は長くなりますが、難しくはないため、落ち着いて理解しましょう。
誤字脱字や何かございましたらご連絡お願いいたします。
スポンサードサーチ
落ちもの系ゲーム開発Par2

Part1で紹介した、今回作成するゲームの概要を改めて説明します。
今回開発するゲームは、テトリスに似ています。テトリスのルールは、以下のような7つのミノと呼ばれるブロックを積み重ねていき、横一列をミノで満たしたらその行が消され得点します。
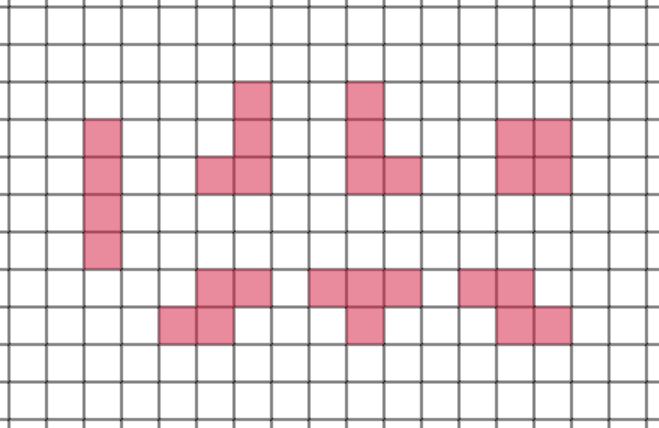
作るゲームの概要
テトリスではミノが消される条件は、「横一列にミノがいっぱいになったら」ですが、今回開発するゲームでは「隣り合うブロックが10になったら」消されるというものです。
ゆえに、ブロック1つひとつには1~9までの数字が代入されます。
以下のような場合、オレンジ色の線で囲まれたブロックが消されます。
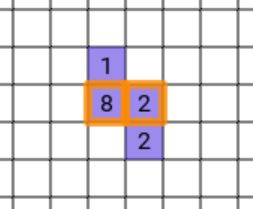
さらに、ブロックが消されたら、その列上で消されたブロックの座標より高い位置にあるブロックは消されたブロックの数だけ下がります。(左図から右図のようになります。)
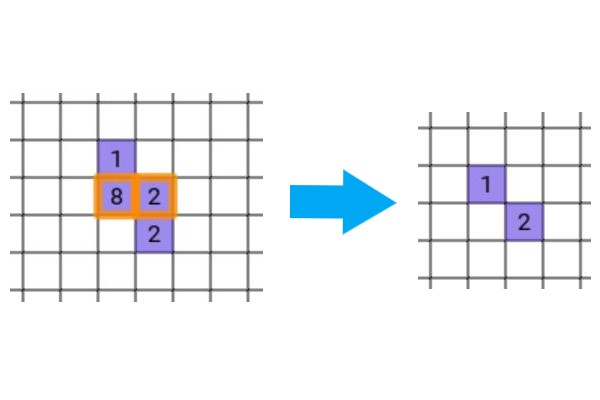
環境開発
OS : Windows10
Python Version : 3.7
Kivy Version : 1.11.1
Numpy Version : 1.18.1
開発手順
1.全てのミノに共通する関数を作成します。(共通の初期値、動作、関数)
2.7種類のミノ(Iミノ、JミノLミノ、Oミノ、Sミノ、Tミノ、Zミノ)を作成します。
3.ブロックの削除関係
4.kivyを使ってアプリケーションを開発します。
1、2、3は4のための準備であるため、簡単です。4は1番ボリュームがあります。
今回は、
共通関数の機能の1つである、ミノを盤面上に固定する関数を作成します。また、7種類のミノを作成します。
ミノを盤面上に固定

Part1で作った「moveMinoPos」を使って、盤面上に表示する座標を取得し、ミノを盤面上に固定していきます。
以下のコードがミノを盤面上に固定する関数です。tenplus.pyに追記します。
# Number 10 plus
import numpy as np
import random
# 共通関数
class CommonFunc():
def __init__(self):
# 省略
def moveMinoPos(self, field, origin=None, block=None):
# 省略
def updateField(self, field):
posList = self.moveMinoPos(field)
for pos in posList:
field[pos[0]] = self.mino[pos[1]]
pass
# 以下省略
コードの解説
12行目から16行目の「updateField」が、ミノを盤面上に固定する関数です。
13行目の「posList = self.moveMinoPos(field)」は、そのミノ自身の基準点を使って、盤面上の座標を求めています。
14、15行目の「for文」は、得られた座標を引数の盤面に固定しています。
posListは、「((盤面上の座標), (ミノの配列上の座標))」となっているため、「pos[0]」によって盤面上の座標を、「pos[1]」によってミノの配列上の座標を選択しています。
この関数の動作確認は7種類のミノを完成させてから行います。
スポンサードサーチ
7種類のミノ

今回開発するゲームで使われるミノは、テトリスで使われる7種類のミノです。下図に示します。
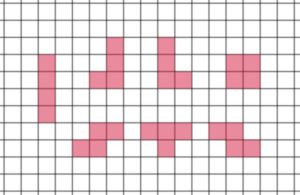
ミノには、盤面に表示させるための基準点が必要となります。また回転などを行うため、ミノのパターンを表現した配列が必要となります。
以下のコードは、7種類のミノを表したソースコードです。tenplus.pyに追記します。
# Number 10 plus
import numpy as np
import random
# 共通関数
class CommonFunc():
# 省略
# Iミノ
class Imino(CommonFunc):
def __init__(self):
super(Imino, self).__init__()
self.base = (1, 4) # fieldにおけるミノの左上の座標
self.count = 0
self.pattern = np.array([[[0, self.n1, 0, 0],
[0, self.n2, 0, 0],
[0, self.n3, 0, 0],
[0, self.n4, 0, 0]],
[[ 0, 0, 0, 0],
[self.n1, self.n2, self.n3, self.n4],
[ 0, 0, 0, 0],
[ 0, 0, 0, 0]],
[[0, 0, self.n4, 0],
[0, 0, self.n3, 0],
[0, 0, self.n2, 0],
[0, 0, self.n1, 0]],
[[ 0, 0, 0, 0],
[ 0, 0, 0, 0],
[self.n4, self.n3, self.n2, self.n1],
[ 0, 0, 0, 0]]])
self.mino = self.pattern[0]
# Jミノ
class Jmino(CommonFunc):
def __init__(self):
super(Jmino, self).__init__()
self.base = (2, 5)
self.count = 0
self.pattern = np.array([[[ 0, self.n1, 0],
[ 0, self.n2, 0],
[self.n4, self.n3, 0]],
[[ 0, 0, 0],
[self.n1, self.n2, self.n3],
[ 0, 0, self.n4]],
[[0, self.n3, self.n4],
[0, self.n2, 0],
[0, self.n1, 0]],
[[self.n4, 0, 0],
[self.n3, self.n2, self.n1],
[ 0, 0, 0]]])
self.mino = self.pattern[0]
# Lミノ
class Lmino(CommonFunc):
def __init__(self):
super(Lmino, self).__init__()
self.base = (2, 4)
self.count = 0
self.pattern = np.array([[[0, self.n1, 0],
[0, self.n2, 0],
[0, self.n3, self.n4]],
[[ 0, 0, self.n4],
[self.n1, self.n2, self.n3],
[ 0, 0, 0]],
[[self.n4, self.n3, 0],
[ 0, self.n2, 0],
[ 0, self.n1, 0]],
[[ 0, 0, 0],
[self.n3, self.n2, self.n1],
[self.n4, 0, 0]]])
self.mino = self.pattern[0]
# Oミノ
class Omino(CommonFunc):
def __init__(self):
super(Omino, self).__init__()
self.base = (2, 4)
self.count = 0
self.pattern = np.array([[[0, 0, 0, 0],
[0, self.n1, self.n2, 0],
[0, self.n3, self.n4, 0],
[0, 0, 0, 0]],
[[0, 0, 0, 0],
[0, self.n2, self.n4, 0],
[0, self.n1, self.n3, 0],
[0, 0, 0, 0]],
[[0, 0, 0, 0],
[0, self.n4, self.n3, 0],
[0, self.n2, self.n1, 0],
[0, 0, 0, 0]],
[[0, 0, 0, 0],
[0, self.n3, self.n1, 0],
[0, self.n4, self.n2, 0],
[0, 0, 0, 0]]])
self.mino = self.pattern[0]
# Sミノ
class Smino(CommonFunc):
def __init__(self):
super(Smino, self).__init__()
self.base = (3, 5)
self.count = 0
self.pattern = np.array([[[ 0, self.n2, self.n1],
[self.n4, self.n3, 0],
[ 0, 0, 0]],
[[self.n1, 0, 0],
[self.n2, self.n3, 0],
[ 0, self.n4, 0]],
[[ 0, 0, 0],
[ 0, self.n3, self.n4],
[self.n1, self.n2, 0]],
[[0, self.n4, 0],
[0, self.n3, self.n2],
[0, 0, self.n1]]])
self.mino = self.pattern[0]
# Tミノ
class Tmino(CommonFunc):
def __init__(self):
super(Tmino, self).__init__()
self.base = (2, 4)
self.count = 0
self.pattern = np.array([[[ 0, 0, 0],
[self.n1, self.n2, self.n3],
[ 0, self.n4, 0]],
[[0, self.n3, 0],
[0, self.n2, self.n4],
[0, self.n1, 0]],
[[ 0, self.n4, 0],
[self.n3, self.n2, self.n1],
[ 0, 0, 0]],
[[ 0, self.n1, 0],
[self.n4, self.n2, 0],
[ 0, self.n3, 0]]])
self.mino = self.pattern[0]
# Zミノ
class Zmino(CommonFunc):
def __init__(self):
super(Zmino, self).__init__()
self.base = (3, 4)
self.count = 0
self.pattern = np.array([[[self.n1, self.n2, 0],
[ 0, self.n3, self.n4],
[ 0, 0, 0]],
[[ 0, self.n4, 0],
[self.n2, self.n3, 0],
[self.n1, 0, 0]],
[[ 0, 0, 0],
[self.n4, self.n3, 0],
[ 0, self.n2, self.n1]],
[[0, 0, self.n1],
[0, self.n3, self.n2],
[0, self.n4, 0]]])
self.mino = self.pattern[0]
# 以下省略
コードの解説
7種類のミノクラスで定義されている変数名は全て同じであるため、その変数名について解説します。重要な変数については個別に解説します。
14、38、58、78、102、122、142行目の「super(クラス名, self).__init__()」は、親クラスである「CommonFunc」で定義されている数字を利用するためのコードです。これによって、「n1、n2、n3、n4」をそのクラスで使うことができます。
15、39、59、79、103、123、143行目の「self.base」は、後述する「self.mino」に代入されている配列の(0, 0)が、盤面上のどこの座標に当たるかを示しています。つまり、ミノの生成時に盤面上のどこに表示させるかを決定しています。
なお、プレイヤーは見ることができない盤面上の(4, 5)の座標を終了判定に利用する関係上、生成時にはミノの一部が(4, 5)に存在するようにbaseを決定しています。

16、40、60、80、104、124、144行目の「self.count」は、後述する「self.pattern」に代入されているミノのパターンを指定するためのものです。
33、53、73、97、117、137、157行目の「self.mino = self.pattern[0]」は、現在のミノの配列が代入されます。後述する「self.pattern」の4つのパターンの中から1つを指定します。
ここから各ミノの「self.pattern」について解説します。self.patternは、指定する数字が大きくなる方向が左回転で、数字が小さくなる方向が右回転です。
しかし、「1→4」または「4→1」に変化する場合は例外です。
17行目から32行目のIミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。

41行目から52行目のJミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。
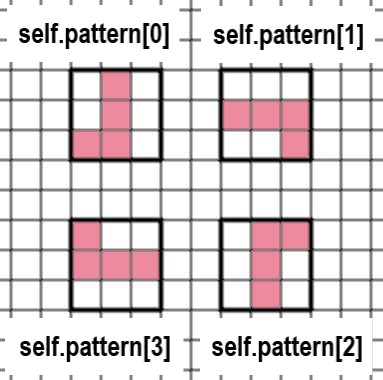
61行目から72行目のLミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。
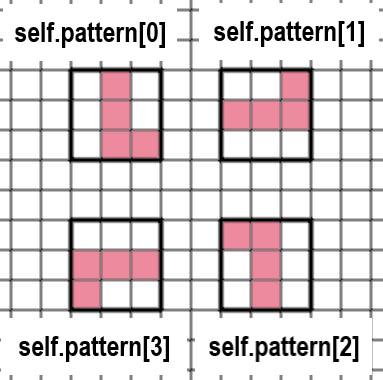
81行目から96行目のOミノの「self.pattern」は、形は変化しませんが、数字は変化します。一応、以下にself.patternを図式化したものを示します。
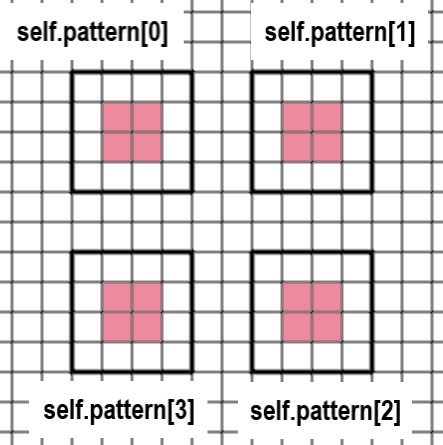
105行目から116行目のSミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。
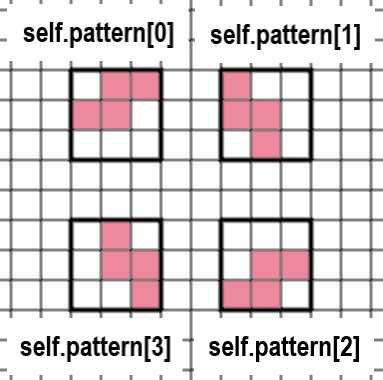
125行目から136行目のTミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。
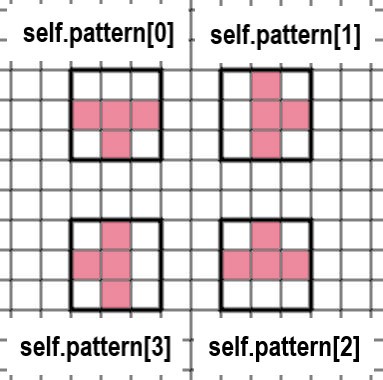
145行目から156行目のZミノの「self.pattern」は、以下のように形が変化します。それにともない、代入されている数字も移動します。以下にself.patternを図式化したものを示します。

動作確認

7種類のミノを作成するこができたため、動作確認を行うことができます。
コマンドプロンプトを起動し、ファイルを保存してあるフォルダまで移動します。移動したら以下のコマンドを入力し、インタプリタを起動させます。
python
インタプリタを起動させたら、tenplus.pyからクラスや盤面をインポートします。以下のコマンドを実行します。
>>> from tenplus import field
>>> from tenplus import Imino, Jmino, Lmino, Omino, Smino, Tmino, Zmino
>>> from tenplus import CommonFunc
以上で準備が整いました。CommonFuncのupdateFieldの動作確認の手順を以下に示します。
1.ミノオブジェクトを生成します。
2.元の盤面を確認するため、fieldを表示させます。
3.生成したミノでupdateFieldを実行します。
4.また、fieldを表示させます。
私は以下のようになりました。
>>> mino = Imino()
>>> field
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 9, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
>>> mino.updateField(field)
>>> field
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 9, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
特定の座標に数字が代入されていれば、動作確認は完了です。また、1だけでなく全てのミノで動作確認を行いましょう。
スポンサードサーチ
まとめ

今回は、7種類のミノと共通関数に盤面にミノを固定する関数を作成しました。
Part1ではコードを動かすことができなかったですが、Part2でようやくコードを動かすことができました。
本記事で作成したコードを以下に示します。
今はまだ、盤面に表示させることしかできませんが、Part3では、共通関数に回転や移動の関数を作成します。
最後までお読みいただきありがとうございます。
スポンサードサーチ
