【Python】Ear Clippingアルゴリズムの実装

こんにちは、にわこまです!
今回はear clippingというアルゴリズムをpythonで実装する方法を紹介します。
本記事で紹介するソースコードを以下に示します。
スポンサードサーチ
Ear Clippingとは

n個の頂点を持つ多角形をn-2個の三角形に分割するアルゴリズムのこと。
イメージを以下に示します。左の図形を右の図のように分割します。
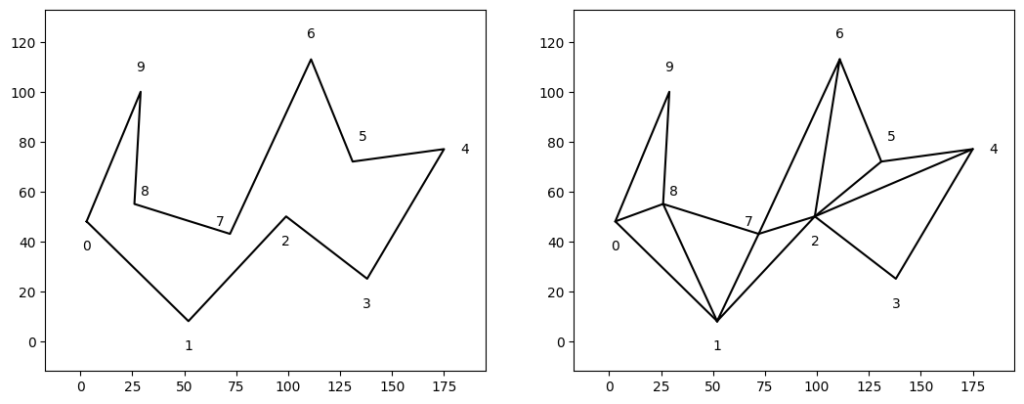
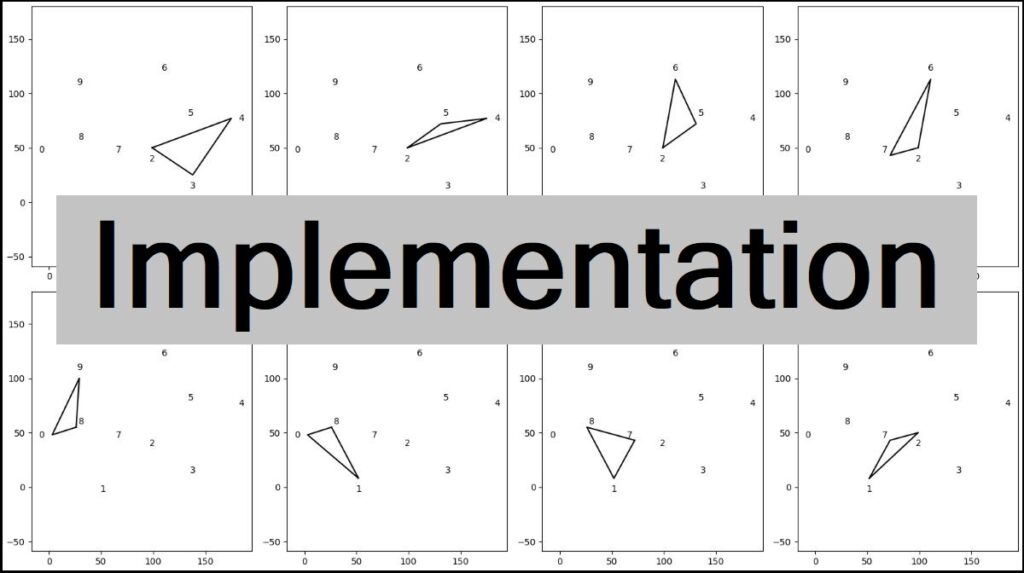
ear clippingの流れを以下に示します。
前提
頂点が4個以上ある多角形を考えます。
頂点は反時計回りの順で番号付けされているとします。
i番目の頂点をViと表現します。
1. Vi-1、Vi、Vi+1で作られる角度が180度未満であるか確認します。・・・条件1
2. Vi-1、Vi、Vi+1で作られる三角形の中に他の頂点が存在しないことを確認します。・・・条件2
3. 条件1と条件2を満たすVi-1、Vi、Vi+1を分割された1つの三角形とします。
4. 頂点のリストからViを削除します。
5. 頂点の数が3未満になるまで繰りかえします。
Ear Clippingの実装
Vi-1、Vi、Vi+1で作られる角度が180度未満であるか確認する方法として、反時計回りであるか確認する方法を採用します。以降時計回り判定と表現します。
実際に角度を計測するということはしません。
なぜ時計回りではなく反時計回りであるか確認するかと言うと、頂点を反時計回りの順で番号付けしているからです。
時計回り判定の方法として数学の外積という知識を使用します。参考サイトはこちら
Vi-1、Vi、Vi+1で作られる三角形の中に他の頂点が存在しないことを確認する方法を以降内外判定と表現します。
内外判定は先ほどの時計回り判定を応用して判定します。内外判定の参考サイトはこちら
Vi-1、Vi、Vi+1で作られる三角形の内、Viの頂点を以降耳先と表現します。
コードの提示
ソースコードを以下に示します。
def cross2d(a, b):
return a[0] * b[1] - b[0] * a[1]
def is_cloclwise(a, b, c):
ab = ((b[0] - a[0]), (b[1] - a[1]))
bc = ((c[0] - b[0]), (c[1] - b[1]))
abc = cross2d(ab, bc)
if (abc < 0):
return True
return False
def is_inside_triangle(v, a, b, c):
abv = is_cloclwise(a, b, v)
bcv = is_cloclwise(b, c, v)
cav = is_cloclwise(c, a, v)
if (abv == bcv == cav):
return True
return False
def is_ear_tip(vertices, i, cw=True):
a = vertices[i - 1]
b = vertices[i]
c = vertices[(i + 1) % len(vertices)]
if (cw != is_cloclwise(a, b, c)):
return False
for v in vertices:
if (v == a or v == b or v == c):
continue
if (is_inside_triangle(v, a, b, c)):
return False
return True
def ear_clipping(vertices):
vs = vertices[:]
triangles = []
while (len(vs) >= 3):
for i in range(len(vs)):
if (is_ear_tip(vs, i, False)):
triangles.append(
[
vs[i - 1],
vs[i],
vs[(i + 1) % len(vs)]
]
)
vs.pop(i)
break
return triangles
# 以下、動作確認用
vertices = [
(3, 48), # 0
(52, 8), # 1
(99, 50), # 2
(138, 25), # 3
(175, 77), # 4
(131, 72), # 5
(111, 113), # 6
(72, 43), # 7
(26, 55), # 8
(29, 100) # 9
]
triangles = ear_clipping(vertices)
print("triangles : {0}".format(triangles))
print("len(triangles) : {0}".format(len(triangles)))
for tri in triangles:
a, b, c = tri
print("{0} : {1}-{2}-{3}".format(
tri,
vertices.index(a),
vertices.index(b),
vertices.index(c)
))
コードの解説
1行目の「cross2d」は、外積を求める関数を定義しています。引数にはベクトルaとベクトルbを代入しています。
2行目では、ベクトルaとベクトルbの外積を求めて返しています。
4行目の「is_clockwise」は、時計回りを判定する関数を定義しています。引数には頂点a、頂点b、頂点cを代入しています。
5行目では、ベクトルabを計算しています。
6行目では、ベクトルbcを計算しています。
7行目では、ベクトルabとベクトルbcの外積を求めています。
9行目では、Trueを返しています。外積の値が0未満である場合は時計回りと判定できるためTrueを返しています。
13行目の「is_inside_triangle」は、内外を判定する関数を定義しています。引数には三角形abcの頂点と内外判定対象の頂点vを代入しています。
14行目では、頂点a、頂点b、頂点vの時計回りを判定しています。
15行目では、頂点b、頂点c、頂点vの時計回りを判定しています。
16行目では、頂点c、頂点a、頂点vの時計回りを判定しています。
18行目では、Trueを返しています。先に求めた時計回り判定結果が全て同じである場合は、三角形abcの中に頂点vが存在すると判定できるためTrueを返しています。
20行目ではFalseを返しています。
22行目の「is_ear_tip」は、耳先を判定する関数を定義しています。引数には頂点のリストと耳先判定対象の頂点が格納されているインデックスと時計回りの方向を代入しています。
23行目では、耳先判定対象の頂点の1つ前の頂点をリストから抽出しています。
24行目では、耳先判定対象の頂点をリストから抽出しています。
25行目では、耳先判定対象の頂点の1つ後の頂点をリストから抽出しています。
28行目では、Falseを返しています。3つの頂点で時計回り判定を実施し引数の時計回りの方向と異なる場合は、3つの頂点で作られる角度が180度以上と判定できるためFalseを返しています。
31行目と32行目では、内外判定対象の頂点を選別しています。
34行目では、Falseを返しています。三角形abcの中に頂点vが存在する場合は、耳先ではないと判定できるためFalseを返してます。
36行目では、Trueを返しています。i番目の頂点を耳先と判定できるためTrueを返しています。
38行目の「ear_clipping」は、ear clipping関数を定義しています。引数には頂点のリストを代入しています。
39行目では、引数の頂点リストをコピーしています。
40行目では、三角形の頂点を代入するリストを定義しています。
42行目から53行目のwhile文は頂点のリストの要素数が3未満になるまで繰り返します。
43行目から52行目のfor文は頂点のリストの要素数だけ繰り返します。
44行目では、耳先を判定しています。判定結果がTrueである場合、45行目以降の処理を実施します。
45行目から51行目では、三角形の頂点をリストに追加しています。
52行目では、頂点のリストから耳先の頂点を削除しています。
53行目では、for文を抜けるためにbreakしています。
54行目では、分割できた三角形の頂点を返しています。
スポンサードサーチ
動作確認

動作確認を実施します。
コードを保存し、コマンドプロンプトを開きます。コードを保存したフォルダまで移動し、以下のコマンドを実行します。
python ear_clipping.py
=====
triangles : [[(99, 50), (138, 25), (175, 77)], [(99, 50), (175, 77), (131, 72)], [(99, 50), (131, 72), (111, 113)], [(99, 50), (111, 113), (72, 43)], [(52, 8), (99, 50), (72, 43)], [(3, 48), (52, 8), (72, 43)], [(3, 48), (72, 43), (26, 55)], [(29, 100), (3, 48), (26, 55)]]
len(triangles) : 8
[(99, 50), (138, 25), (175, 77)] : 2-3-4
[(99, 50), (175, 77), (131, 72)] : 2-4-5
[(99, 50), (131, 72), (111, 113)] : 2-5-6
[(99, 50), (111, 113), (72, 43)] : 2-6-7
[(52, 8), (99, 50), (72, 43)] : 1-2-7
[(3, 48), (52, 8), (72, 43)] : 0-1-7
[(3, 48), (72, 43), (26, 55)] : 0-7-8
[(29, 100), (3, 48), (26, 55)] : 9-0-8
元の図形と分割後の図形を以下に示します。

まとめ

今回は、ear clippingというアルゴリズムをpythonで実装する方法を紹介しました。
ear clippingは「n個の頂点を持つ多角形をn-2個の三角形に分割するアルゴリズムのこと。」です。
本記事で紹介したソースコードを以下に示します。
参考
・ear clippingの論文
Triangulation by Ear Clipping
・内外判定
三角形の外積
・javascriptでear clippingを実装しているyoutube
Triangulating a polygon with JavaScript | ear clipping algorithm implementation
最後までお読みいただきありがとうございます。
スポンサードサーチ
