オセロのアルゴリズム比較 Part2

おはようございます!にわこまです。今回はpythonでつくった8×8のオセロでアルゴリズムの比較を行いました。
何かご指摘があればご連絡ください!
スポンサードサーチ
アルゴリズム比較 Part2
前回(アルゴリズム比較Part1)は、4×4のオセロでアルゴリズムを比較しました。
しかし、4×4のオセロでは後手がかなり有利であるため、ほとんど比べる意味がありませんでした。
ゆえに、今回は8×8のオセロでアルゴリズムの比較を行いました。
8×8のオセロであれば、アルゴリズムの強さや弱さ、相性が分かるのではないかと思いました。
前回と同じアルゴリズムですが、比較したアルゴリズムを紹介します。
・「ひっくり返す石を多くする」
・「ひっくり返す石を少なくする」
・「自分が打った手に対して相手の打つ手を多くなする」
・「自分が打った手に対して相手の打つ手を少なくする」
前回と同じ、上記4つのアルゴリズムで比較を行いました。
4つのアルゴリズム
改めてアルゴリズムを紹介します。
・「ひっくり返す石を多くする」
・「ひっくり返す石を少なくする」
・「自分が打った手に対して相手の打つ手を多くする」
・「自分が打った手に対して相手の打つ手を少なくする」
上2つのアルゴリズムは、まず現状の盤面で打つことのできるマスを導き出します。そのマス、1つひとつに石を打ったと仮定し、ひっくり返した石の数を数えます。これの結果に応じて手を選びます。
下2つのアルゴリズムは、まず現状の盤面で打つことのできるマスを導き出します。そのマス、1つひとつに石を打ったと仮定します。更新された盤面において相手の打つことのできる手の数を数えます。
注意
・ひっくり返す石の数や打つことのできる手の数が同数の場合は、配列上1番若いものを選びます。
・よって、同じ組み合わせのアルゴリズムを何回対局させても結果が変わりません。
例:「ひっくり返す石を多くする」VS「ひっくり返す石を少なくする」の対局を行っても、最終盤面や棋譜は全く変わりません。
対局の組み合わせを紹介します。(1つの組み合わせで先手後手を入れ替えます。)
・「ひっくり返す石を多くする」VS「ひっくり返す石を少なくする」
・「自分が打った手に対して相手の打つ手を少なくする」VS「自分が打った手に対して相手の打つ手を多くする」
・「ひっくり返す石を多くする」VS「自分が打った手に対して相手の打つ手を多くする」
・「ひっくり返す石を多くする」VS「自分が打った手に対して相手の打つ手を少なくする」
・「ひっくり返す石を少なくする」VS「自分が打った手に対して相手の打つ手を多くする」
・「ひっくり返す石を少なくする」VS自分が打った手に対して相手の打つ手を少なくする」
6つの組み合わせで、先手後手を入れ替えて計12回の対局の比較を行います。 組み合わせと最終盤面を書いていきます。
スポンサードサーチ
結果
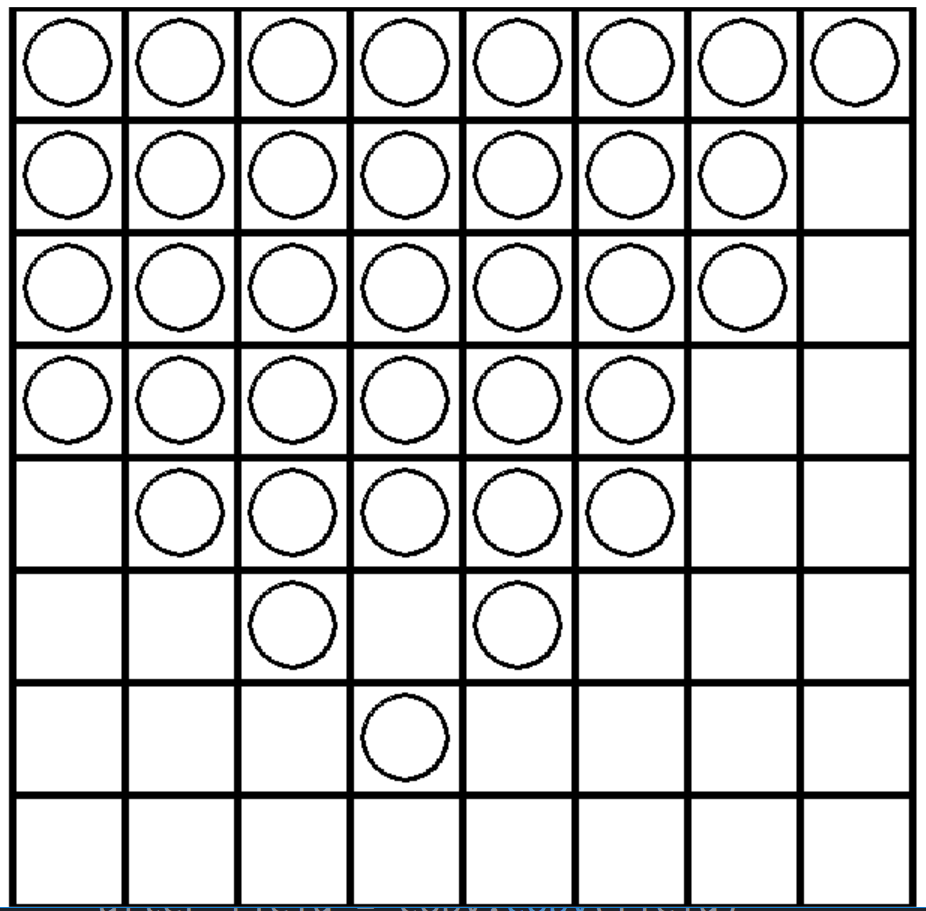
対戦の組み合わせと対戦終了後の盤面を示します。
・先手「ひっくり返す石を多くする」VS後手「ひっくり返す石を少なくする」
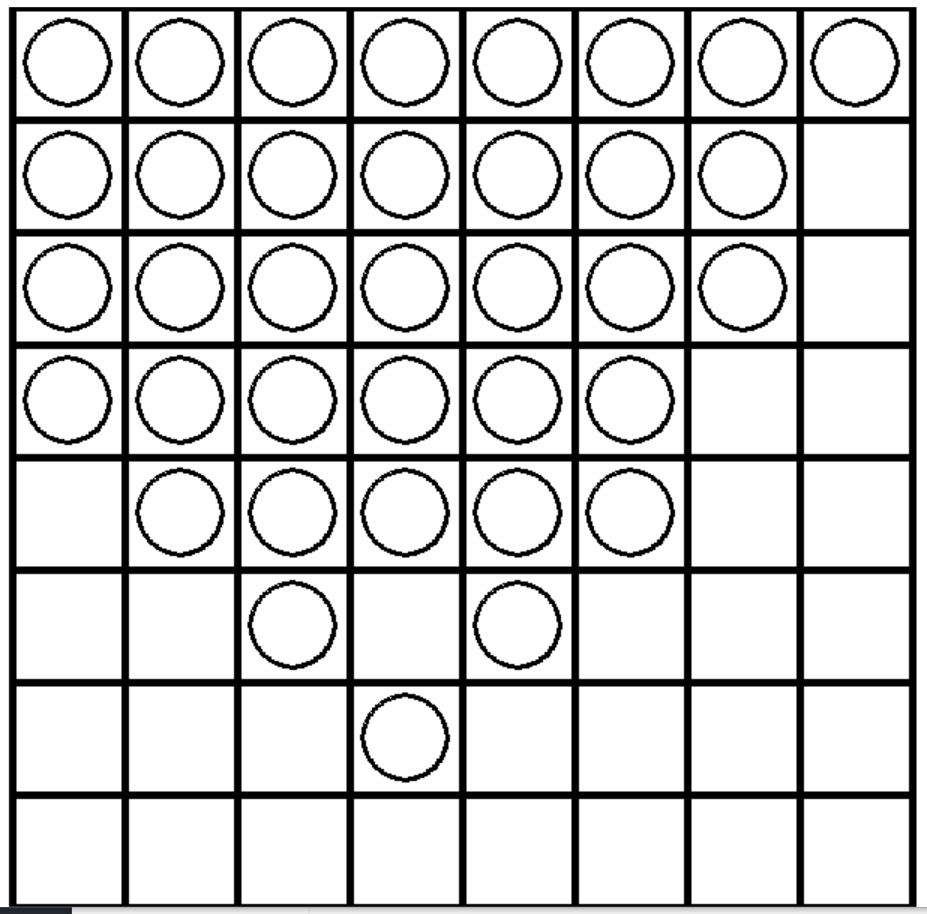
・後手「ひっくり返す石を多くする」VS先手「ひっくり返す石を少なくする」
・先手「自分が打った手に対して相手の打つ手を少なくする」VS後手「自分が打った手に対して相手の打つ手を多くする」
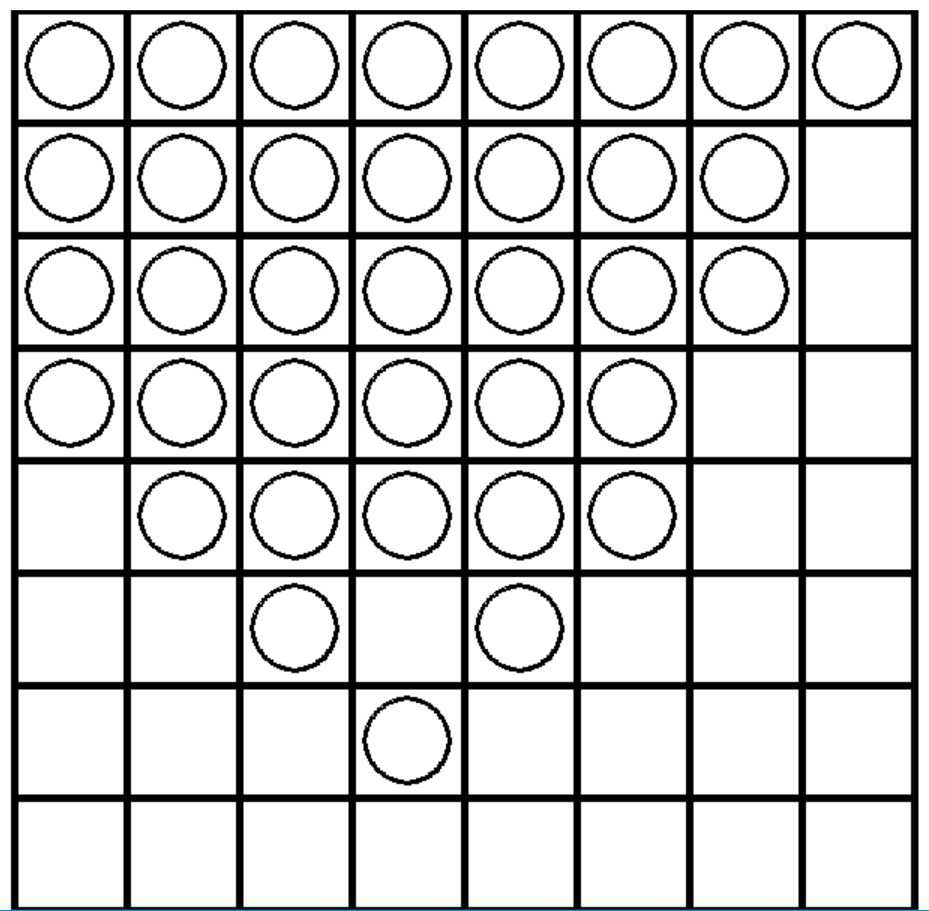
・後手「自分が打った手に対して相手の打つ手を少なくする」VS先手「自分が打った手に対して相手の打つ手を多くする」
・先手「ひっくり返す石を多くする」VS後手「自分が打った手に対して相手の打つ手を多くする」
・後手「ひっくり返す石を多くする」VS先手「自分が打った手に対して相手の打つ手を多くする」
・先手「ひっくり返す石を多くする」VS後手「自分が打った手に対して相手の打つ手を少なくする」
・後手「ひっくり返す石を多くする」VS先手「自分が打った手に対して相手の打つ手を少なくする」
・先手「ひっくり返す石を少なくする」VS後手「自分が打った手に対して相手の打つ手を多くする」
・後手「ひっくり返す石を少なくする」VS先手「自分が打った手に対して相手の打つ手を多くする」
・先手「ひっくり返す石を少なくする」VS後手「自分が打った手に対して相手の打つ手を少なくする」
・後手「ひっくり返す石を少なくする」VS先手「自分が打った手に対して相手の打つ手を少なくする」
結果まとめ
A. 「ひっくり返す石を多くする」
B. 「ひっくり返す石を少なくする」
C. 「自分が打った手に対して相手の打つ手を多くする」
D. 「自分が打った手に対して相手の打つ手を少なくする」
| A 後手 | B 後手 | C 後手 | D 後手 | |
| A 先手 | × | 36-0 (pass) | 0-36 (pass) | 0-36 (pass) |
| B 先手 | 36-0 (pass) | × | 0-36 (pass) | 0-36 (pass) |
| C 先手 | 22-42 | 22-42 | × | 22-42 |
| D 先手 | 28-36 | 28-36 | 36-28 | × |
今回の結果から推測すると、
1番強いアルゴリズムは、「自分が打った手に対して相手の打つ手を少なくする」であると考えられます。
逆に1番弱いアルゴリズムは、「自分が打った手に対して相手の打つ手が多くなる」であると考えられます。
結局後手有利
今回の結果を見ると、後手が有利であると思われるかもしれません。
しかし、後手が有利に見えるのには理由がいくつかあります。
1つ目は、アルゴリズムにおいて、「ひっくり返す石の数」や「打つことのできる手の数」が同数の場合は、配列上1番若いものを選択するようにしてあるからです。
これにより対戦結果の盤面が固定されています。
2つ目は、盤面の評価値を考慮していないため、本来ならば置かないような場所にも置いてしまうからです。
これにより、安易に角を取らせてしまいます。
3つ目は、対戦回数が少ないからです。1つ目と2つ目を改善できれば、この3つ目は解決できます。
ゆえに、まだまだアルゴリズムが不完全であり、信用できるほどの結果が得られていないということです。
スポンサードサーチ
まとめ
今回は、pythonでつくった8×8のオセロでどのアルゴリズムが強いか弱いか検証してみました。
結果としては、「自分が打った手に対して相手の打つ手を少なくする」というアルゴリズムが1番強いアルゴリズムに見えました。
たいして、「自分が打った手に対して相手の打つ手が多くなる」というアルゴリズムが1番弱いアルゴリズムに見えました。
しかし、アルゴリズムが不完全であるため、信用できる結果ではありませんでした。
アルゴリズムの種類を増やすとともに、今回比較したアルゴリズムを改善して、アルゴリズムの比較を続けていきたいと思います。
最後までお読みいただきありがとうございます。
スポンサードサーチ