【Kivy】Pythonで落ちもの系ゲーム開発(テトリス風)Part1

こんにちは、にわこまです。
今回は、kivyとpythonを使って落ちもの系ゲームを開発していきます。落ちもの系ゲームと言えばテトリスやぷよぷよが有名ですが、今回開発するのは、テトリスに近い落ちもの系ゲームです。本記事では、作るゲームの概要や共通関数の一部を作成します。
誤字脱字や分からない点がございましたらご連絡お願いいたします。
スポンサードサーチ
落ちもの系ゲーム開発Part1

落ちもの系・積みもの系ゲームと聞いて、最初に思い浮かぶのはテトリスやぷよぷよ、6ボールだと思います。
今回開発するゲームは、テトリスに1番似ています。テトリスのルールは、以下のような7つのミノと呼ばれるブロックを積み重ねていき、横一列をミノで満たしたらその行が消され得点します。
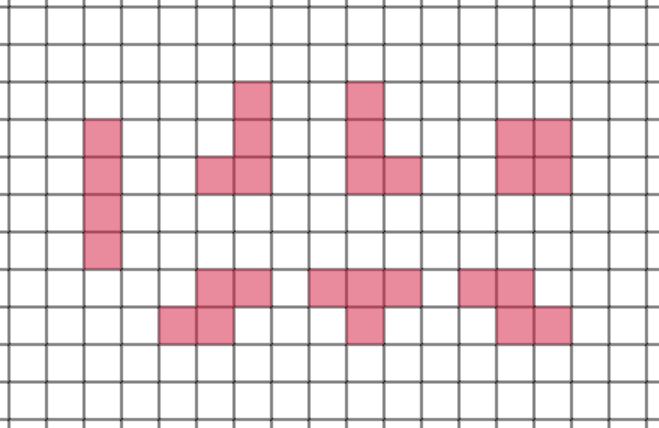
作るゲームの概要
テトリスではミノが消される条件は、「横一列にミノがいっぱいになったら」ですが、今回開発するゲームでは「隣り合うブロックが10になったら」消されるというものです。
ゆえに、ブロック1つひとつには1~9までの数字が代入されます。
以下のような場合、オレンジ色の線で囲まれたブロックが消されます。
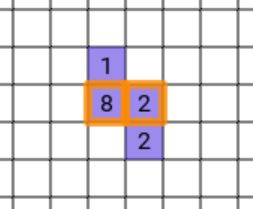
さらに、ブロックが消されたら、その列上で消されたブロックの座標より高い位置にあるブロックは消されたブロックの数だけ下がります。(左図から右図のようになります。)
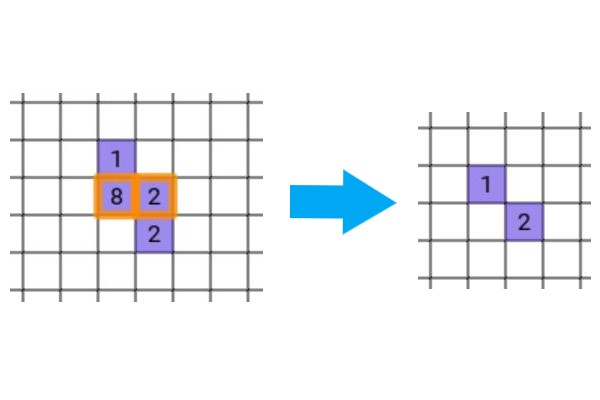
開発環境
OS : Windows10
Python Version : 3.7
Kivy Version : 1.11.1
Numpy Version : 1.18.1
pythonやkivyのバージョンが分からない場合は、コマンドプロンプトを開きpythonのインタプリタを起動させます。起動させたら以下のコマンドを実行します。
# pythonのバージョン確認
import sys
sys.version
# kivyのバージョン確認
import kivy
kivy.__version__
開発手順
1.全てのミノに共通する関数を作成します。(共通の初期値、動作、関数)
2.7種類のミノ(Iミノ、JミノLミノ、Oミノ、Sミノ、Tミノ、Zミノ)を作成します。
3.ブロックの削除関係
4.kivyを使ってアプリケーションを開発します。
1、2、3は4のための準備であるため、簡単です。4は1番ボリュームがあります。
今回は
共通関数の数字と盤面の特定の位置にミノを移動させることが可能か調べる関数を作成します。
共通関数

共通関数(CommonFunc)では、7種類全てのミノに共通する初期値や機能を作成します。共通すると考えたものは、以下のようになります。
1.数字(ブロック1つひとつに代入する)
2.盤面の特定の位置にミノを移動させることができるか調べ、できた場合にその座標を返す関数
3.右回転が可能か調べる関数
4.左回転が可能か調べる関数
5.右への移動が可能か調べる関数
6.左への移動が可能か調べる関数
7.下への移動が可能か調べる関数
8.盤面に数字を固定する関数
以上の8つが共通する初期値や関数であると考えました。
その中でも本記事では、1番目と2番目を作成します。
「1.数字」は、下図のようにブロック1つひとつに割り当てられる数字を1~9の中からランダムに生成します。
「2.盤面の特定の位置にミノを移動させることができるか調べ、できた場合にその座標を返す関数」は、3~7の関数の回転や移動に使用します。
スポンサードサーチ
CommonFunc

共通関数を「CommonFunc」として定義し、上記で説明した初期値と関数を作成します。
tenplus.pyを作成し、以下のコードを書きこみます。
# Number 10 plus
import numpy as np
import random
# 共通関数
class CommonFunc():
def __init__(self):
self.n1 = random.randrange(1, 10)
self.n2 = random.randrange(1, 10)
self.n3 = random.randrange(1, 10)
self.n4 = random.randrange(1, 10)
def moveMinoPos(self, field, origin=None, block=None):
if(origin == None):
origin = self.base
if(type(block) != np.ndarray):
block = self.mino
row, col = np.shape(block)
rowMax, colMax = np.shape(field)
rowBase, colBase = origin
posList = []
for i in range(0, row):
for j in range(0, col):
num = block[(i, j)]
rpos = rowBase + i
cpos = colBase + j
if(num != 0):
if(0 > rpos or rpos > rowMax-2 or 1 > cpos or cpos > colMax-2):
return []
if(field[(rpos, cpos)] != 0):
return []
posList.append(((rpos, cpos), (i, j)))
return posList
global field
field = np.array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 1
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 5
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 10
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 15
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 20
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10], # 25
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
if __name__ == '__main__':
pass
コードの解説
2行目の「import numpy as np」と3行目の「import random」は、本コードで使用するライブラリをインポートしています。
7行目から33行目の「CommonFunc」は、共通関数です。
8行目から12行目の「__init__」は、ブロック1つひとつに代入する数字を生成しています。
13行目から33行目の「moveMinoPos」は、盤面の特定の位置にミノを移動させることが出来るか調べ、できたらその座標を返す関数です。
「moveMinoPos」について説明します。
まず、引数についてです。引数は「field」、「origin=None」、「block=None」となっています。
fieldは、盤面のことです。実際にミノを移動させたり固定したりする場所です。fieldはこの関数を実行する際は、毎回指定します。
originは、配列として指定されている各ミノの(0, 0)の座標がfieldでは、どの座標を指すか指定するものです。左右と下方向へ移動できるか確認するときに指定します。
下図を用いて説明します。左図はIミノを表していて、左上の座標は(0, 0)です。しかし右図の盤面では、(2, 4)となります。この(2, 4)が各ミノのbaseと呼ばれる変数に代入します。さらにその変数をoriginに指定することで移動できるかを指定します。
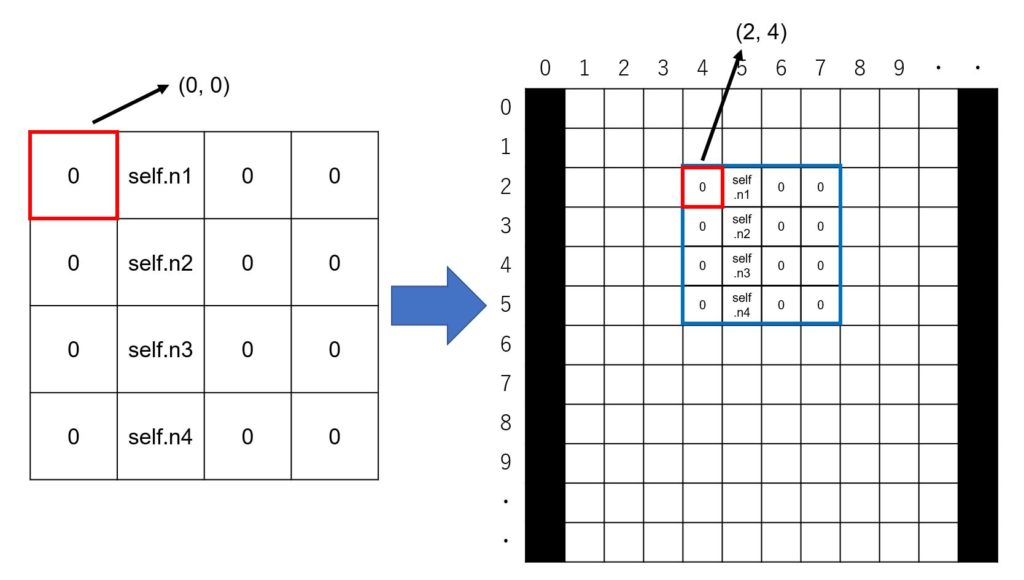
blockは、各ミノの配列を指定します。上図の左のような配列を指定します。右回転、左回転ができるか確認するときに指定します。
14、15行目は、引数にoriginが指定されているか調べ、指定されていなければそのミノ自身の基準点(self.base)を指定します。
16、17行目は、引数にblockが指定されているか調べ、指定されていなければそのミノ自身の配列(self.mino)を指定します。
18行目の「row, col = np.shape(block)」は、blockの行と列の大きさをそれぞれrowとcolに代入しています。
19行目の「rowMax, colMax = np.shape(field)」は、盤面の行と列の大きさをそれぞれrowMaxとcolMaxに代入しています。
20行目の「rowBase, colBase = origin」は、盤面上の基準点をそれぞれrowBaseとcolBaseに代入しています。
21行目の「posList = []」は、ブロックが盤面上に位置する座標のリストです。しかし、このリストには次のように代入されます。((盤面上の座標), (ミノ自身の配列における座標))です。
22行目から32行目は、ミノ自身の配列を左上から指定していき、数字が代入されている座標が盤面上ではどの位置に存在するか確かめるループ文です。
24行目の「num = block[(i, j)]」は、ミノ自身の配列において(i, j)の座標にある数字をnumに代入しています。
25行目の「rpos = rowBase + i」と26行目の「cpos = colBase + j」は、24行目で得られた数字が盤面上のどの座標に存在するか導き出し、それぞれrposとcposに代入しています。
下図のように基準点が分かれば、数字が代入されている座標が分かるようになっています。
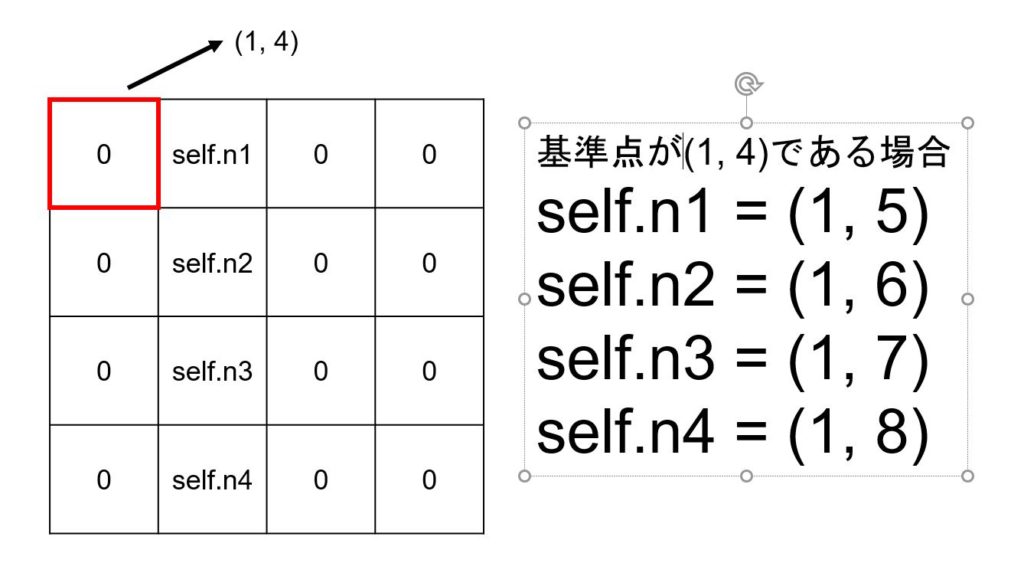
27行目の「IF文」は、24行目で得られた数字が0以外の数字であるか判定しています。(ブロックに代入される数字は1~9であるため。)
28行目の「IF文」は、盤面上に存在する座標として算出された「rpos」と「cpos」が有効範囲内に存在していないことを確かめる条件です。
「存在していない」ということが1回でも真になるとき、そのミノは盤面上のその座標に移動できないということになるため、「存在している」という条件よりも「存在していない」という条件でIF文を記述しています。
縦方向(rpos)の条件は、「0よりも小さい」と「rowMax-2(24)より大きい」の2つです。
横方向(cpos)の条件は、「1よりも小さい」と「colMax-2(10)より大きい」の2つです。
rowMaxとcolMaxは、1から数えています。しかし、配列は0から指定します。ゆえに、配列の最大を指定したい場合は、rowMaxまたはcolMaxからは、1引かなくてはいけません。なおかつ盤面には壁が設定してあるため盤面上の最大値は、さらにrowMaxまたはcolMaxからは1引かなくてはいけません。
ゆえに、「rowMax – 2」や「colMax – 2」という条件になっています。
29行目の「return []」は、28行目のIF文によってミノが盤面上に移動できないことが証明されたため、空のリストを返しています。
30行目の「IF文」は、盤面上の座標(rpos, cpos)にブロックが存在していることを確かめる条件です。「!= 0」つまり、これから移動しようとする座標に1~9の数字があることを確認します。
移動しようとする座標に1~9の数字が「存在している(!= 0)」ということが1回でも真になるとき、その座標に移動できないことの証明になるため、1~9の数字が「存在していない(== 0)」という条件よりも1~9の数字が「存在している(!= 0)」という条件でIF文を記述しています。
31行目の「return []」は、30行目のIF文によってミノが盤面上に移動できないことが証明されたため、空のリストを返しています。
32行目の「return posList」は、盤面上の座標とミノの配列上の座標がペアになって格納されているリストが返されます。
36行目から62行目は、グローバル変数として盤面を生成しています。盤面は12行26列で生成しています。
動作確認
各ミノクラスを作成していないため動作確認が行えません。次回以降で動作確認を行います。
まとめ

今回は、テトリスのような落ちものゲームを作成するということで、各ミノに共通する関数の一部を作成しました。
具体的に動かしていないため、分かりにくかったと思います。今回に関して理解できていなくても問題ありません。Part2以降で具体的に動かしていき確認していきます。
本記事で作成したコードを以下に示します。
Part2では、各ミノを作成します。共通関数はまだ完成していませんが、ミノクラスが完成していないと確認できないことが多いため、先に各ミノを作成します。
最後までお読みいただきありがとうございます。
スポンサードサーチ
