【Kivy】Pythonで落ちもの系ゲーム開発(テトリス風)Part3

こんにちは、にわこまです。
今回は、ミノを動かす関数を作成します。具体的には、CommonFuncの左回転、右回転、左移動、右移動、下移動の5つの関数を作成します。関数自体は簡単なため、実際に盤面でどのように動作するかをしっかり確認しましょう。
誤字脱字など何かございましたらご連絡お願いいたします。
スポンサードサーチ
落ちもの系ゲーム開発Par3

Part1で紹介した、今回作成するゲームの概要を改めて説明します。
今回開発するゲームは、テトリスに似ています。テトリスのルールは、以下のような7つのミノと呼ばれるブロックを積み重ねていき、横一列をミノで満たしたらその行が消され得点します。
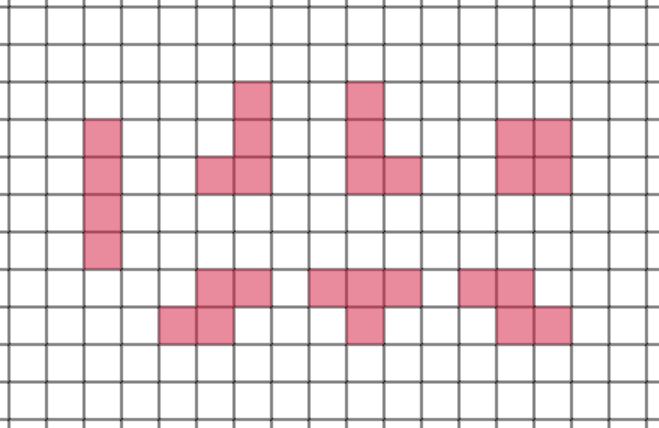
作るゲームの概要
テトリスではミノが消される条件は、「横一列にミノがいっぱいになったら」ですが、今回開発するゲームでは「隣り合うブロックが10になったら」消されるというものです。
ゆえに、ブロック1つひとつには1~9までの数字が代入されます。
以下のような場合、オレンジ色の線で囲まれたブロックが消されます。
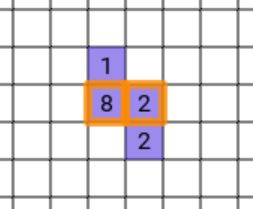
さらに、ブロックが消されたら、その列上で消されたブロックの座標より高い位置にあるブロックは消されたブロックの数だけ下がります。(左図から右図のようになります。)
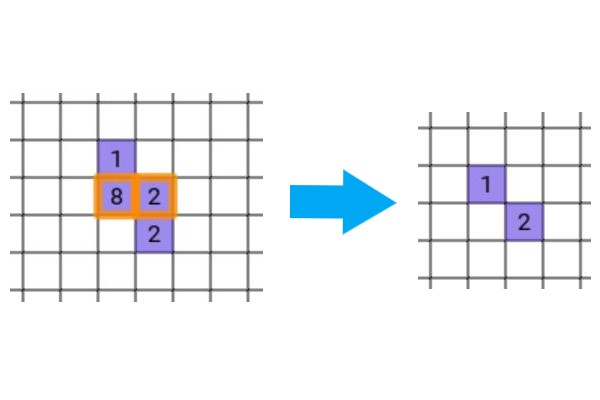
開発環境
OS : Windows10
Python Version : 3.7
Kivy Version : 1.11.1
Numpy Version : 1.18.1
開発手順
1.全てのミノに共通する関数を作成します。(共通の初期値、動作、関数)
2.7種類のミノ(Iミノ、JミノLミノ、Oミノ、Sミノ、Tミノ、Zミノ)を作成します。
3.ブロックの削除関係
4.kivyを使ってアプリケーションを開発します。
1、2、3は4のための準備であるため、簡単です。4は1番ボリュームがあります。
今回は、
共通関数(CommonFunc)を完成させます。
左回転と右回転

左回転と右回転は、各ミノのcountを増やしたり減らしたりすることで実現します。私が作成したミノの回転は、テトリスの回転とは異なります。
以下は、左回転と右回転のソースコードです。tenplus.pyに追記します。
# Number 10 plus
import numpy as np
import random
# 共通関数
class CommonFunc():
def __init__(self):
# 省略
def moveMinoPos(self, field, origin=None, block=None):
# 省略
def updateField(self, field):
# 省略
def rollLeft(self, field):
block = self.pattern[(self.count + 1) % 4]
posList = self.moveMinoPos(field, block=block)
if(len(posList) != 0):
self.count = (self.count + 1) % 4
self.mino = self.pattern[self.count]
return True
return False
def rollRight(self, field):
block = self.pattern[(self.count + 3) % 4]
posList = self.moveMinoPos(field, block=block)
if(len(posList) != 0):
self.count = (self.count + 3) % 4
self.mino = self.pattern[self.count]
return True
return False
# 以下省略
コードの解説
14行目から21行目の「rollLeft」は、ミノの左回転を実現する関数です。引数はfield(盤面)となっています。返却値は、TrueまたはFalseとなります。正しく回転出来た場合はTrue、回転できなければFalseが返されます。
15行目の「block」は、ミノを左に90度回転させた配列を代入します。
patternのインデックスは「(self.count + 1) % 4」のように指定しています。4で割った余りを指定しています。インデックスは0~3の範囲であるためです。
16行目の「posList」は、ミノの盤面における座標を代入します。moveMinoPosには、fieldとblockを指定します。
17行目の「IF文」は、posListに座標があることを判定しています。盤面上にミノを置くことが出来ない場合は、posListが空になるためこのような条件にしています。
18行目の「self.count」は、15行目で指定したインデックスを代入しています。
19行目の「self.mino」は、回転後の配列を代入しています。
20行目の「return True」は、正しく回転することが出来たためTrueを返却します。
21行目の「return False」は、回転が出来なかったためFalseを返却しています。
22行目から29行目の「rollRight」は、ミノの右回転を実現する関数です。引数はfield(盤面)となっています。返却値は、TrueまたはFalseとなります。正しく回転出来た場合はTrue、回転できなければFalseが返されます。
23行目の「block」は、ミノを右に90度回転させた配列を代入します。
patternのインデックスは「(self.count – 1) % 4」のように指定しています。4で割った余りを指定しています。インデックスは0~3の範囲であるためです。
24行目の「posList」は、ミノの盤面における座標を代入します。moveMinoPosには、fieldとblockを指定します。
25行目の「IF文」は、posListに座標があることを判定しています。盤面上にミノを置くことが出来ない場合は、posListが空になるためこのような条件にしています。
26行目の「self.count」は、23行目で指定したインデックスを代入しています。
27行目の「self.mino」は、回転後の配列を代入しています。
28行目の「return True」は、正しく回転することが出来たためTrueを返却します。
29行目の「return False」は、回転が出来なかったためFalseを返却しています。
動作確認
コマンドプロンプトを開き、ファイルが保存してあるフォルダまで移動します。移動したら以下のコマンドを入力し、インタプリタを実行します。
python
1.tenplus.pyから必要なクラスクラスなどをインポートします。以下のコマンドを実行します。
>>> from tenplus import CommonFunc, field
>>> from tenplus import Imino, Jmino, Lmino, Omino, Smino, Tmino, Zmino
>>> import numpy as np
2.盤面のコピーを生成し、そのコピー盤面にミノを表示させます。私の場合、以下のように表示されました。
>>> copyfield = np.copy(field)
>>> mino = Imino()
>>> mino.updateField(copyfield)
>>> copyfield
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 5, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
3.ミノを回転させ、元の盤面に表示します。私の場合は、以下のように表示されました。
>>> mino.rollLeft(field)
True
>>> mino.updateField(field)
>>> field
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 6, 5, 5, 1, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
回転していることを確認できたら、動作確認は完了です。他のミノでもためしてみてください。
スポンサードサーチ
左移動と右移動と下移動

ミノの移動に関する関数ではself.baseを変化させることで、盤面にミノを表示可能か判定します。
以下は、移動に関する関数のソースコードです。tenplus.pyに追記します。
# Number 10 plus
import numpy as np
import random
# 共通関数
class CommonFunc():
def __init__(self):
# 省略
def moveMinoPos(self, field, origin=None, block=None):
# 省略
def updateField(self, field):
# 省略
def rollLeft(self, field):
# 省略
def rollRight(self, field):
# 省略
def moveLeft(self, field):
origin = (self.base[0], self.base[1]-1)
posList = self.moveMinoPos(field, origin=origin)
if(len(posList) != 0):
self.base = (self.base[0], self.base[1]-1)
return True
return False
def moveRight(self, field):
origin = (self.base[0], self.base[1]+1)
posList = self.moveMinoPos(field, origin=origin)
if(len(posList) != 0):
self.base = (self.base[0], self.base[1]+1)
return True
return False
def moveUnder(self, field):
origin = (self.base[0]+1, self.base[1])
posList = self.moveMinoPos(field, origin=origin)
if(len(posList) != 0):
self.base = origin
return True
return False
# 以下省略
コードの解説
18行目から24行目の「moveLeft」は、1つ左へ移動するための関数です。引数はfield(盤面)となっています。返却値は、TrueまたはFalseとなります。正しく移動出来た場合はTrue、移動できなければFalseが返されます。
19行目の「origin」は、self.baseを1つ左へ移動させた座標を代入します。1つ左へ移動とは、列から1を引くことです。
20行目の「posList」は、ミノの盤面における座標を代入します。moveMinoPosには、fieldとoriginを指定します。
21行目の「IF文」は、posListに座標があることを判定しています。盤面上にミノを置くことが出来ない場合は、posListが空になるためこのような条件にしています。
22行目の「self.base」は、1つ左へ移動させた座標を代入します。
23行目の「return True」は、正しく移動することが出来たためTrueを返却します。
24行目の「return False」は、移動が出来なかったためFalseを返却しています。
25行目から31行目の「moveLeft」は、1つ右へ移動するための関数です。引数はfield(盤面)となっています。返却値は、TrueまたはFalseとなります。正しく移動出来た場合はTrue、移動できなければFalseが返されます。
26行目の「origin」は、self.baseを1つ右へ移動させた座標を代入します。1つ右へ移動とは、列に1を足すことです。
27行目の「posList」は、ミノの盤面における座標を代入します。moveMinoPosには、fieldとoriginを指定します。
28行目の「IF文」は、posListに座標があることを判定しています。盤面上にミノを置くことが出来ない場合は、posListが空になるためこのような条件にしています。
29行目の「self.base」は、1つ右へ移動させた座標を代入します。
30行目の「return True」は、正しく移動することが出来たためTrueを返却します。
31行目の「return False」は、移動が出来なかったためFalseを返却しています。
32行目から38行目の「moveUnder」は、1つ下へ移動するための関数です。引数はfield(盤面)となっています。返却値は、TureまたはFalseとなります。正しく移動出来た場合はTrue、移動できなければFalseが返されます。
33行目の「origin」は、self.baseを1つ下へ移動させた座標を代入します。1つ下へ移動とは、行に1を足すことです。
34行目の「posList」は、ミノの盤面における座標を代入します。moveMinoPosには、fieldとoriginを指定します。
35行目の「IF文」は、posListに座標があることを判定しています。盤面上にミノを置くことが出来ない場合は、posListが空になるためこのような条件にしています。
36行目の「self.base」は、1つ下へ移動させた座標を代入します。
37行目の「return True」は、正しく移動することが出来たためTrueを返却します。
38行目の「return False」は、移動が出来なかったためFalseを返却しています。
動作確認
コマンドプロンプトを開き、ファイルが保存してあるフォルダまで移動します。移動したら以下のコマンドを入力し、インタプリタを実行します。
python
1.tenplus.pyから必要なクラスクラスなどをインポートします。以下のコマンドを実行します。
>>> from tenplus import CommonFunc, field
>>> from tenplus import Imino, Jmino, Lmino, Omino, Smino, Tmino, Zmino
>>> import numpy as np
2.盤面のコピーを生成し、そのコピー盤面にミノを表示させます。私の場合、以下のように表示されました。
>>> copyField = np.copy(field)
>>> mino = Imino()
>>> mino.updateField(copyField)
>>> copyField
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 3, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 4, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
3.2~3回ほど左へ移動して、元の盤面に表示させます。私の場合は、以下のように表示されました。
>>> mino.moveLeft(field)
True
>>> mino.moveLeft(field)
True
>>> mino.moveLeft(field)
True
>>> mino.updateField(field)
>>> field
array([[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 3, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 6, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 4, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 10],
[10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]])
左へ移動していることが確認できたら、動作確認は完了です。
同様に、moveRightやmoveUnderの動作確認もしてみてください。さらに、他のミノでの確認してみてください。
まとめ

今回は、ミノの回転や移動に関する関数を作成しました。今は、何もない盤面で動作確認をしたましたが、適当に数字を配置した盤面でも動作確認をしてみると面白いかもしれません。
本記事で作成したコードを以下に示します。
次回Part4では、ブロックの削除する関数を作成します。
最後までお読みいただきありがとうございます。
スポンサードサーチ
