【Python】マッチ棒クイズ開発 Part8

こんにちは、にわこまです。
今回は、当たり判定について2つの関数を作成します。具体的に言うと棒部分の当たり判定の関数と火薬部分の当たり判定の関数を作成します。当たり判定の関数は数学的要素があり、少し難しめです。数学苦手な方はコードをダウンロードしてPart9をお楽しみください。
誤字脱字や分からない点がございましたらご連絡お願いいたします!
メールまたはTwitterのDMまで!!
マッチ棒クイズ開発の目次はこちら
スポンサードサーチ
棒部分の当たり判定

棒部分は長方形になります。そのため、与えられた座標がその長方形内であるかどうかを判定する関数を作成することになります。
マッチ棒は回転するため、長方形の方向は縦方向、横方向、斜め方向(左上から右下、右上から左下)になります。
以下にイメージ図を示します。

基本的には、青色の線で囲まれたベージュの範囲内であるかを判定します。
その範囲は、「x軸方向の最小と最大の間であるか」と「y軸方向の最小と最大の間にあるか」で判定できます。
しかし、斜め方向の判定では不十分です。
そのため、与えられた座標が「①と②の線の上方にあり、③と④の線の下方にある」という条件を追加する必要があります。
コードの提示
マッチ棒の棒部分の当たり判定を判定する関数のソースコードを以下に示します。
import kivy
kivy.require("2.0.0")
from kivy.app import App
from kivy.uix.floatlayout import FloatLayout
from kivy.uix.widget import Widget
from kivy.graphics import Color, Rectangle, Ellipse
from kivy.graphics import Rotate
from kivy.graphics.context_instructions import PushMatrix, PopMatrix
import numpy as np
class MatchStickWidget(Widget):
def __init__(self, ms_w, angle, **kwargs):
super(MatchStickWidget, self).__init__(**kwargs)
self.size = [0, 0]
self.past_pos = (0, 0)
#self.before_move_pos = (0, 0)
self.ms_w = ms_w
self.create_property("angle", value=angle)
self.origin = (self.x + self.ms_w / 2, self.y + self.ms_w * 6.8 / 2)
# Rotate Theta
self.theta = np.radians(self.angle)
self.new_x = lambda t: (t[0] - self.origin[0]) * round(np.cos(self.theta), 3) - (t[1] - self.origin[1]) * round(np.sin(self.theta), 3) + self.origin[0]
self.new_y = lambda t: (t[0] - self.origin[0]) * round(np.sin(self.theta), 3) + (t[1] - self.origin[1]) * round(np.cos(self.theta), 3) + self.origin[1]
self.new_points = lambda t, o=(0, 0): (self.new_x(t) + o[0], self.new_y(t) + o[1])
# Stick
self.posStick = [self.x+self.ms_w*0.2, self.y]
self.sizeStick = [self.ms_w * 0.6, self.ms_w * 5.6]
self.pointsStick = [(self.posStick[0] + [0, self.sizeStick[0], 0, self.sizeStick[0]][i], # Added
self.posStick[1] + [0, 0, self.sizeStick[1], self.sizeStick[1]][i]) for i in range(4)] # Added
self.rotatedPointsStick = sorted([self.new_points(point) for point in self.pointsStick], key=lambda t: t[1]) # Added
# Powder
self.posPowder = [self.x, self.y+self.ms_w*5.2]
self.sizePowder = [self.ms_w, self.ms_w*1.6]
#self.pointsPowder = [(self.posPowder[0] + [0, self.sizePowder[0], 0, self.sizePowder[0]][i],
# self.posPowder[1] + [0, 0, self.sizePowder[1], self.sizePowder[1]][i]) for i in range(4)]
with self.canvas:
PushMatrix()
self.rot = Rotate()
self.rot.angle = self.angle
self.rot.origin = self.origin
Color(rgb=[0.96, 0.87, 0.7])
self.stick = Rectangle(pos=self.posStick, size=self.sizeStick)
Color(rgb=[0.8, 0.1, 0])
self.powder = Ellipse(pos=self.posPowder, size=self.sizePowder)
PopMatrix()
self.bind(pos=self.drawMS)
self.bind(angle=self.rotateTheta)
def rotateTheta(self, *args):
self.rot.angle = self.angle
self.theta = np.radians(self.angle) # Added
self.rotatedPointsStick = sorted([self.new_points(point) for point in self.pointsStick], key=lambda t: t[1]) # Added
def collide_point_stick(self, touch, *args):
fml = lambda a, t: a * (touch[0] - t[0]) + t[1]
xmini, xmax = min([p[0] for p in self.rotatedPointsStick]), max([p[0] for p in self.rotatedPointsStick])
ymini, ymax = min([p[1] for p in self.rotatedPointsStick]), max([p[1] for p in self.rotatedPointsStick])
if((xmini <= touch[0] and touch[0] <= xmax
and ymini <= touch[1] and touch[1] <= ymax)
and ((fml(-1, self.rotatedPointsStick[0]) <= touch[1] and fml(1, self.rotatedPointsStick[0]) <= touch[1]
and touch[1] <= fml(-1, self.rotatedPointsStick[3]) and touch[1] <= fml(1, self.rotatedPointsStick[3]))
or round(self.rotatedPointsStick[0][1]) == round(self.rotatedPointsStick[1][1]))):
return True
return False
def on_touch_down(self, touch, *args):
#tof = (self.collide_point_stick(touch.pos) or self.collide_point_powder(touch.pos))
tof = self.collide_point_stick(touch.pos) # Added
if(touch.is_double_tap and tof):
self.angle += 45
return True
elif(not(touch.is_double_tap) and tof):
touch.grab(self)
self.past_pos = touch.pos
return True
return False
def on_touch_up(self, touch, *args):
# 省略
def on_touch_move(self, touch, *args):
# 省略
def drawMS(self, *args):
# rot
self.origin = (self.x + self.ms_w / 2, self.y + self.ms_w * 6.8 / 2)
self.rot.origin = self.origin
# stick
self.posStick = [self.x+self.ms_w*0.2, self.y]
self.pointsStick = [(self.posStick[0] + [0, self.sizeStick[0], 0, self.sizeStick[0]][i], # Added
self.posStick[1] + [0, 0, self.sizeStick[1], self.sizeStick[1]][i]) for i in range(4)] # Added
self.stick.pos = self.posStick
self.rotatedPointsStick = sorted([self.new_points(point) for point in self.pointsStick], key=lambda t: t[1]) # Added
# powder
self.posPowder = [self.x, self.y+self.ms_w*5.2]
#self.pointsPowder = [(self.posPowder[0] + [0, self.sizePowder[0], 0, self.sizePowder[0]][i],
# self.posPowder[1] + [0, 0, self.sizePowder[1], self.sizePowder[1]][i]) for i in range(4)]
self.powder.pos = self.posPowder
def collide_center_circle(self, wid, *args):
# 省略
class RootWidget(FloatLayout):
def __init__(self, **kwargs):
super(RootWidget, self).__init__(**kwargs)
with self.canvas.before:
Color(rgb=[1, 1, 1])
self.bg_rect = Rectangle(pos=self.pos, size=self.size)
def on_size(self, *args):
self.bg_rect.size = self.size
class MatchStickQuizApp(App):
def build(self):
root = RootWidget()
root.add_widget(MatchStickWidget(25, 0, pos=[100, 100]))
return root
if __name__ == '__main__':
MatchStickQuizApp().run()
pass
上記のコードは以下からダウンロードできます。
コードの解説
23行目の「self.theta」は、angleをラジアン単位に変更した角度が代入されている変数です。以下の無名関数内で使用します。
24行目から26行目の「無名関数」は、回転後の座標を求める関数です。
24行目の「self.new_x」は、x座標がself.theta分だけ回転したときの座標を算出する関数です。
25行目の「self.new_y」は、y座標がself.theta分だけ回転したときの座標を算出する関数です。
26行目の「self.new_points」は、先述したself.new_xとself.new_yを使って、回転後の座標を算出する関数です。
以下のサイトを参考にして関数を作成しました。
回転移動の1次変換はこちら
30行目と31行目の「self.pointsStick」は、初期位置の4つ角の座標が代入されているリスト型の変数です。
32行目の「self.rotatedPointsStick」は、回転後の座標をy座標の昇順かつy座標が同じである場合はx座標の昇順に並び替えた4つ角の座標が代入されているリスト型の変数です。
例を次に示します。「(0, 0), (100, 0), (0, 50), (100, 50), 」。
52行目の「self.theta」は、angleを再びラジアン単位に変換された値が代入されています。self.thetaの更新を行っています。
53行目の「self.rotatedPointsStick」は、回転後の座標を再算出された値が並び替えられて代入されています。self.rotatedPointsStickの更新を行っています。
54行目から64行目の「collide_point_stick関数」は、棒部分の当たり判定を判定する関数です。引数にtouchが必要となります。
55行目の「fml」は、直線の方程式「y = ax + b」のyを求める無名関数です。引数はa(傾き)とx、b(回転後の座標)です。
56行目の「xmini」と「xmax」は、回転後の座標におけるx座標の最小と最大が代入されている変数です。min関数とmax関数で求めています。
57行目の「ymini」と「ymax」は、回転後の座標におけるy座標の最小と最大が代入されている変数です。min関数とmax関数で求めています。
58行目から62行目の「if文」は、実際に当たり判定を判定している条件式です。
58行目と59行目では、クリックされた座標が「x軸方向の最小と最大の間であるか」と「y軸方向の最小と最大の間にあるか」を判定しています。
60行目では、クリックされたy座標が①と②の線の上方にあることを判定しています。
61行目では、クリックされたy座標が③と④の線の下方になることを判定しています。
62行目では、self.rotatedPointsStickの0番目と1番目のy座標が同値であるかを判定しています。
この判定では、現在のマッチ棒の方向を確認しています。60行目61行目は斜め方向のときだけ判定したいため、縦方向と横方向の時は常にTrueを返すようにしています。
63行目の「return文」は、Trueを返しています。
64行目の「return文」は、Falseを返しています。
68行目の「tof」は、collide_point_stick関数のTrueまたはFalseが代入されている変数です。
87行目と88行目の「self.pointsStick」は、移動後の4つ角の座標が代入されているリスト型の変数です。
90行目の「self.rotatedPointsStick」は、回転後の座標が代入されたリスト型の変数です。
動作確認
コードを保存したら、コマンドプロンプトを開きファイルを保存したフォルダまで移動します。移動したら、以下のコマンドを入力し実行します。
python matchstickquiz.py
棒部分をダブルクリックするとマッチ棒が回転することを確認できたら動作確認完了です。


また、棒の部分をクリックして動かすことができることを確認できたら動作確認完了です。
火薬部分の当たり判定

火薬部分は楕円形になります。そのため、与えられた座標がその楕円形内であるかどうかを判定する関数を作成することになります。
マッチ棒は回転するため、楕円形の方向は縦方向、横方向、斜め方向(左上から右下、右上から左下)になります。
以下にイメージ図を示します。

基本的には、青色の線で囲まれた赤色の範囲内であるかを判定します。
その範囲は、楕円の方程式より以下の式(1)で判定できます。
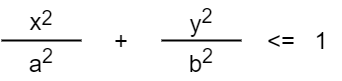
しかし、斜め方向の判定では不十分です。
そのため、角度θだけ回転した楕円の方程式より以下の式(2)で判定を行います。
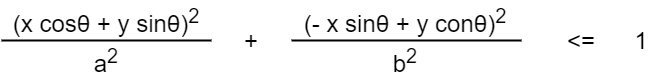
上記の(2)の式で(1)の式も表現できるため、(2)の式のみを使って判定を行います。
コードの提示
マッチ棒の火薬部分の当たり判定の判定を行うソースコードを以下に示します。
import kivy
kivy.require("2.0.0")
from kivy.app import App
from kivy.uix.floatlayout import FloatLayout
from kivy.uix.widget import Widget
from kivy.graphics import Color, Rectangle, Ellipse
from kivy.graphics import Rotate
from kivy.graphics.context_instructions import PushMatrix, PopMatrix
import numpy as np
class MatchStickWidget(Widget):
def __init__(self, ms_w, angle, **kwargs):
# 省略
def rotateTheta(self, *args):
# 省略
def collide_point_stick(self, touch, *args):
# 省略
def collide_point_powder(self, touch, *args):
origin_elli = self.new_points((self.origin[0], self.posPowder[1] + self.sizePowder[1] / 2)) # 楕円の中心座標
num_x = ((touch[0] - origin_elli[0]) * np.cos(self.theta) + (touch[1] - origin_elli[1]) * np.sin(self.theta))**2
num_y = ((touch[1] - origin_elli[1]) * np.cos(self.theta) - (touch[0] - origin_elli[0]) * np.sin(self.theta))**2
value = num_x / (self.sizePowder[0]/2)**2 + num_y / (self.sizePowder[1]/2)**2
if(value <= 1):
return True
return False
def on_touch_down(self, touch, *args):
tof = (self.collide_point_stick(touch.pos) or self.collide_point_powder(touch.pos))
if(touch.is_double_tap and tof):
self.angle += 45
return True
elif(not(touch.is_double_tap) and tof):
touch.grab(self)
self.past_pos = touch.pos
return True
return False
def on_touch_up(self, touch, *args):
# 省略
def on_touch_move(self, touch, *args):
# 省略
def drawMS(self, *args):
# 省略
def collide_center_circle(self, wid, *args):
# 省略
class RootWidget(FloatLayout):
def __init__(self, **kwargs):
super(RootWidget, self).__init__(**kwargs)
with self.canvas.before:
Color(rgb=[1, 1, 1])
self.bg_rect = Rectangle(pos=self.pos, size=self.size)
def on_size(self, *args):
self.bg_rect.size = self.size
class MatchStickQuizApp(App):
def build(self):
root = RootWidget()
root.add_widget(MatchStickWidget(25, 0, pos=[100, 100]))
return root
if __name__ == '__main__':
MatchStickQuizApp().run()
pass
上記のコードは以下からダウンロードできます。
コードの解説
20行目から27行目の「collide_point_powder関数」は、火薬部分の当たり判定を判定する関数です。引数にtouchが必要となります。
21行目の「origin_elli」は、角度θだけ回転したときの楕円の中心の座標が代入されている変数です。イメージを以下に示します。
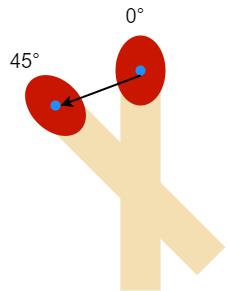
22行目の「num_x」は、式(2)における左の項の分子を計算した値が代入されている変数です。
23行目の「num_y」は、式(2)における右の項の分子を計算した値が代入されている変数です。
斜めの楕円の公式は以下のサイトを参考にしました。
高校数学の美しい物語:斜めの楕円の方程式(特に45度回転)はこちら
式(2)のx、yにはそれぞれクリックされたx座標、y座標が代入されます。しかし、楕円の中心がorigin_elli分だけずれているため、origin_elli分だけx座標、y座標から引いて代入します。
24行目の「value」は、式(2)の左辺を計算した値だ代入されている変数です。
25行目の「if文」は、valueが1以下であるかを判別している条件式です。
26行目の「return文」は、Trueを返しています。
27行目の「return文」は、Falseを返しています。
29行目の「tof」は、collide_point_stickとcollide_point_powderの論理和を行った論理値が代入されている変数です。
スポンサードサーチ
動作確認

コードを保存したら、コマンドプロンプトを開きファイルを保存したフォルダまで移動します。移動したら、以下のコマンドを入力し実行します。
python matchstickquiz.py
棒部分をダブルクリックするとマッチ棒が回転することを確認できたら動作確認完了です。


また、棒の部分をクリックして動かすことができることを確認できたら動作確認完了です。
まとめ

今回は、当たり判定について2つの関数を作成しました。具体的に言うと棒部分の当たり判定の関数と火薬部分の当たり判定の関数を作成しました。
マッチ棒(MatchStickWidget)に関しては今回で完成です。
若干、数学要素があったため難しかったかもしれません。しかし、今後オブジェクトを使って何かを開発したいと思っているなら理解しておくべきだと思います。
次回Part9では、マッチ棒の枠を作成します。以下の画像におけるグレーの部分です。
白地にマッチ棒だけを置いていたら、どこにマッチ棒を動かしよいのか分からなくなるため、予め動かす場所にマッチ棒の枠を置いておきます。
マッチ棒クイズ開発の目次はこちら
最後までお読みいただきありがとうございます。
スポンサードサーチ
